Tutoriel JavaScript : Créer un langage de programmation

Je vous propose dans cette vidéo de découvrir les bases à connaitre pour commencer à créer son propre langage de programmation.

Sommaire

• 00:00 Introduction
• 04:00 Création du lexer
• 12:09 Génération de l'AST
• 18:54 L'interpréteur
• 24:36 Priorité des opérations
• 28:13 Gestion des parenthèses
• 30:40 Gestion des "statements"
• 39:44 Gestion des variables
• 48:05 Gestion des nombres négatifs
• 52:09 Conclusion

Les étapes principales

La création d'un langage de programmation peut sembler intimidante, mais elle suit en réalité un processus bien défini. Bien que nous n'allons pas créer le prochain Python, comprendre ces mécanismes est essentiel pour de nombreux projets (si vous devez implémenter un système de formules dans un tableur par exemple).

Étape 1 : Le Lexer

Travailler à partir d'une chaîne de caractères n'est pas du tout évident lorsqu'il s'agit d'interpréter un langage. Aussi, on va utiliser un lexer (ou analyseur lexical) dont le rôle est de transformer une chaîne de caractères en une série de "jetons" (tokens) qui ont un sens pour notre langage.

Prenons un exemple simple :

A = 1 + 2

Le lexer va identifier :

• A comme un identifiant
• = comme un opérateur d'assignation
• 1 comme un nombre
• + comme un opérateur arithmétique
• 2 comme un nombre

Les jetons et leur nature dépendra du type de langage que vous souhaitez développer, plus votre langage est complexe, plus il y aura de jetons de types différents.

Étape 2 : Le Parser et l'AST

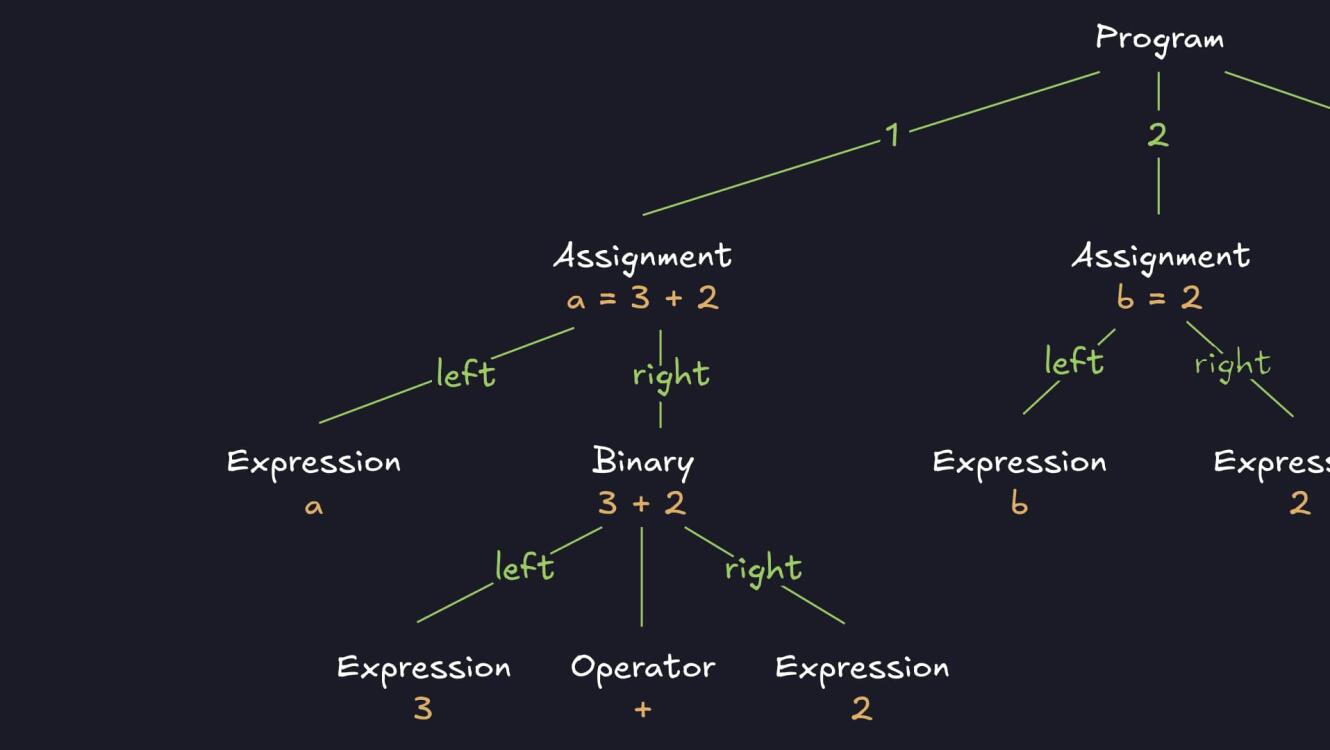
Une fois nos jetons identifiés, le parser entre en jeu pour construire un AST (Abstract Syntax Tree). L'AST est une représentation arborescente de notre programme qui va grandement simplifier son exécution.

Pour visualiser un AST, vous pouvez utiliser AST Explorer, un outil qui permet d'explorer la structure d'arbre pour différents langages.

Dans notre exemple précédent, l'AST ressemblerait à :

graph TD
    A[Program 'A = 1 + 2'] --> B[AssignmentExpression]
    B --> C[Identifier 'A']
    B --> D[BinaryExpression '+']
    D --> E[Number '1']
    D --> F[Number '2']

La beauté de l'AST réside dans sa capacité à représenter des expressions de plus en plus complexes. Si nous ajoutons une opération supplémentaire comme A = 1 + 2 + 3, l'arbre s'adapte naturellement pour représenter cette nouvelle complexité.

graph TD
    A[Program] --> B[AssignmentExpression]
    B --> C[Identifier 'A']
    B --> D[BinaryExpression '+']
    D --> E[BinaryExpression '+']
    D --> F[Number '3']
    E --> G[Number '1']
    E --> H[Number '2']

La création de cet arbre permet ensuite d'exécuter le code plus simplement, mais peut servir aussi à d'autres choses.

• La transpilation (conversion d'un langage vers un autre)
• Le formatage de code (on regénère le code, avec des règles de formatages spécifiques)
• La génération de bytecode pour améliorer les performances (comme dans PHP par)
• La compilation vers du code machine

Mais, dans le cadre de cette vidéo, on va directement interpréter l'AST.

Étape 3 : L'Interpréteur

La dernière étape consiste à interpréter notre AST. L'interpréteur va parcourir l'arbre et exécuter chaque nœud selon sa nature :

• Pour une assignation, il éxécute l'expression et sauvegarde le résultat dans un espace mémoire associé au nom de la variable.
• Pour une expression binaire, il évalue les 2 expressions et applique ensuite l'opérateur
• Et ainsi de suite pour chaque type de nœud

Encore une fois, la complexité de l'interpréteur va beaucoup dépendre du type de langage que l'on cherche à créer, plus il y a de types de nœuds au niveau de l'AST, plus il y aura de complexité au niveau de l'interpréteur.

Pour aller plus loin

Si vous voulez pousser encore plus les choses, je vous invite à vous rendre sur Crafting Interpreters qui détaille en profondeur la création d'un interpréteur et qui détaille des concepts plus complexes comme le ByteCode ou la gestion de la mémoire.